
Energy Resources & Petroleum Engineering Program
Faculty and students in the Energy Resources and Petroleum Engineering (ERPE) Program at KAUST engage in interdisciplinary research to understand and model hydro-chemo-thermo-mechanical coupled processes in the subsurface, with emphasis on multiphase and reactive fluid flow (oil, gas, brine, water and steam).
The Energy Resources and Petroleum Engineering Program focuses on modern reservoir description, engineering and management. Students in this program receive broad training in basic scientific concepts, geology, geophysical characterization, and reservoir engineering. Our Students participate in scientific research activities that may include mathematical analyses, computational modeling, and/or laboratory/field studies. Ph.D. candidates focus on original research driven to advance the boundaries of knowledge.
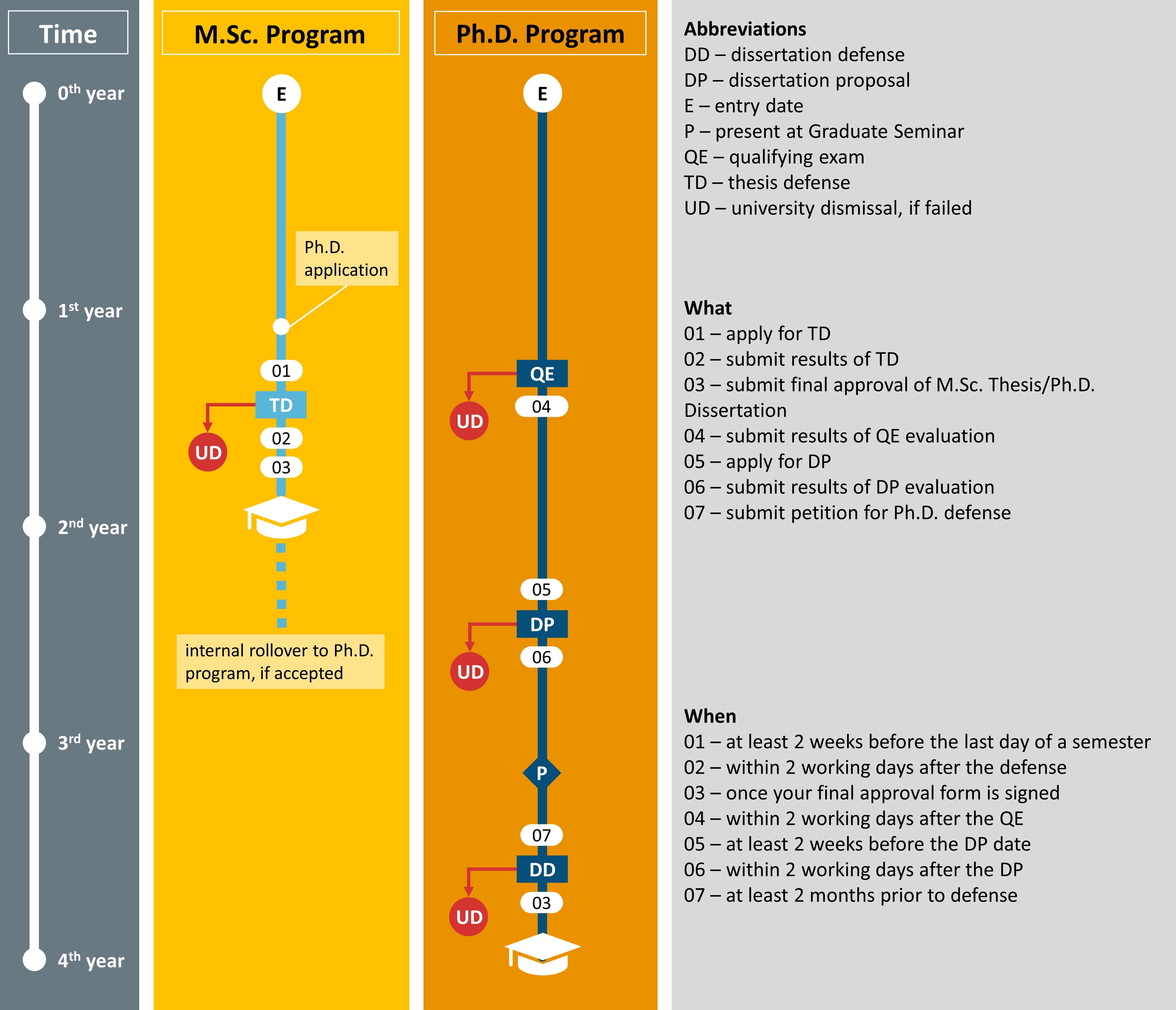
Summary of M.Sc. and Ph.D. Requirements:

Summary of Program Timelines:
Assessment Test
Students are admitted to KAUST from a wide variety of programs and backgrounds. In order to facilitate the design of an appropriate study plan for each individual student, all incoming M.Sc. students will be required to take a written assessment during orientation week. There is no grade for the assessment. The purpose of the assessment is to determine whether students have mastered the prerequisites for undertaking graduate level courses taught in the program. The Academic Advisor uses the results of the assessments to design, if necessary, a remedial study plan with a list of courses aimed at addressing content areas that may impede a student from successful completion of the degree requirements.
Students are encouraged to prepare for the assessment by refreshing the general knowledge gained from their undergraduate education before arriving at KAUST.
Students will be tested on the following subjects:
- Engineering Mathematics
- Physics and Mechanics
- Chemistry and Thermodynamics
Each examination is 25 minutes long, consists of 12 multiple choice questions, and are taken one after the other in the week before the semester formally starts. All examinations are taken online using your KAUST Blackboard account.
In the following sections, you can find an outline of the material covered in each of these examinations.
1. Concept of the limit and its properties. The calculation of limits. One- and two-sided limits.
Continuity. The Intermediate Value Theorem.
2. Definition of the derivative. Differentiation from first principles. Derivatives for standard
functions including the exponential, logarithmic, trigonometric, and hyperbolic functions.
Product, quotient, and chain rules. Higher-order derivatives. Derivatives of inverse
functions. Implicit and parametric differentiation. The Mean Value Theorem and Rolle’s
theorem. Differentiability.
3. Application of the derivative to finding the gradient of a tangent to a curve. Stationary
points. Maxima and minima problems. The differential and its application to errors. Rates of
change problems.
4. The primitive function and anti-differentiation. The indefinite integral. Techniques of
integration including substitution, parts, partial fractions, trigonometric substitutions, and t-
substitutions.
5. The definite integral and Riemann integration. Application of the integral to area and
volume. The first and second Fundamental Theorems of Calculus. Improper integrals.
6. Sequences and infinite series. The geometric and telescoping series. Alternating series.
Convergence and divergence of an infinite series. Test for convergence including the nth
term test, direct and limit comparison tests, the integral test, ratio and root tests, alternating
series test. Absolute and conditional convergence. The Alternating Series Estimation
Theorem.
7. Power series. Properties of power series. Radius of convergence. Taylor and Maclaurin
series. Application of power series. Taylor polynomials.
8. Complex numbers, Argand diagram, modulus-argument and polar forms, de Moivre’s
theorem, exponential form.
9. Vectors. Vector addition and multiplication by a scalar. Properties of vectors. Unit vectors
and direction angles. The scalar dot and vector cross products and their associated
properties. The scalar triple product. Vector identities. Application of vectors to three-
dimensional analytic geometry. Equations of lines and planes in space.
Recommended Reading Material
1. Calculus, J. Stewart. Eight Edition (2015, Cengage Learning).
2. How to Integrate It: A Practical Guide to Finding Elementary Integrals, S. M. Stewart
(2018, Cambridge University Press).
Physics component
1. Electric charge. Electric fields. Coulomb's law.
2. Gauss’ law and applications of this law.
3. Electric potential. Capacitance and dielectrics.
4. Current, resistance, and resistivity.
5. Direct current circuits. Voltmeters and ammeters (both ideal and real). RC circuits.
6. Magnetic fields. Gauss’ law for magnetism.
7. Magnetic forces. Sources of the magnetic field. The Biot-Savart law and Ampère’s
law.
8. Electromagnetic induction. Faraday’s law. Lenz’ law.
9. Displacement current. Maxwell’s equations.
Mechanics component
1. Statics of particles. Forces and moments (torques).
2. Equilibrium of rigid bodies. Centres of mass and centroids
3. Moments of inertia.
4. Stress and strain due to axial loading. Torsion
5. Pure bending. Beam analysis
6. Kinematics of particles (using energy and momentum methods). Newton’s second
law.
7. Planar kinematics of rigid bodies.
8. Planar kinetics of rigid bodies (using equations of motion and energy and momentum
methods).
Recommended Reading Material
1. Sears and Zemanskys University Physics: With Modern Physics. Young, H. D., Freedman,
R. A., Ford, A. L., and Sears, F. W. (Addison-Wesley, 2021).
2. Vector Mechanics for Engineers: Statics and Dynamics (Twelfth edition). Ferdinand P. Beer,
E. Russell Johnston, David F. Mazurek, Phillip J. Cornwall, and Brian P. Self (McGraw-Hill,
2019).
Chemistry component
1. Matter and energy. What is chemistry? Atoms, molecules, and ions. Substances, ele-
ments, and mixtures. Changes and properties of matter. Periodic Table, Periodic Law.
Chemistry divisions. The International Union of Pure and Applied Chemistry (IUPAC).
2. Scientific method: observation, law, hypothesis, experiment, data, results, and theory.
Accuracy and precision. Significant figures. Scientific notation. Basic experimental
quantities. Unit conversion. Basic statistics for data analysis.
3. Timeline of atomic theories and models. Elementary particles. Quantum numbers for
different orbitals. Electron configuration of atoms. Valence electrons and the octet rule.
4. Atomic/ionic radius. Electron affinity. Electronegativity. Ionization energy.
Polarizability. Isoelectronic configurations.
5. Lewis structures. Covalent, ionic, and metallic bonds.
6. Molecular geometry. The valence shell electron pair repulsion (VSEPR) theory.
7. Intermolecular interactions. Phase changes. Gaseous, liquid, and solid states.
Thermodynamics component
1. Fundamentals of thermodynamics.
2. Work and heat. The zeroth and first laws of thermodynamics.
3. Pure substances.
4. The second law of thermodynamics.
5. An ideal gas.
6. Carnot cycle.
7. Entropy.
Recommended Reading Material
1. Denniston, K. J.; Topping, J. J.; Dorr, D. R. Q.; Caret, R. L., General, Organic, and
Biochemistry, McGraw-Hill, 10th edition, 2020.
2. Smoot, R. C.; Smith, R. G.; Price, J., Chemistry: A Modern Course, Merrill Publishing
Company, 1990.
3. Chang, R.; Overby, J., Chemistry, McGraw-Hill, 13th edition, 2019.
4. Goldberg, D. E., Fundamentals of Chemistry, McGraw-Hill, 5th edition, 2007.
5. Gaffney, J.; Marley, N., General Chemistry for Engineers, Elsevier, 1st edition, 2018.
6. Çengel, Y. A.; Boles, M. A., Thermodynamics: An Engineering Approach, McGraw-Hill, 5th
edition, 2006.
Courses
Core Courses provide students with the background needed to establish a solid foundation in the program area. Students must complete 12 credits (4 Core Courses) and be aware that Core Courses may be offered only once per academic year.
| ERPE 200 | Energy and the Environment | 3 |
| ERPE 210 | Fundamentals of Carbonate Geology | 3 |
| ERPE 211 | Data Integration for Geomodelling | 3 |
| ERPE 220 | Sediments: Properties and Processes | 3 |
| ERPE 221 | Geoscience Fundamentals | 3 |
| ERPE 230 | Rock Mechanics for Energy Geo-Engineering | 3 |
| ERPE 240 | Fractals, Percolation and Pore-scale Flow | 3 |
| ERPE 241 | Multiphase Flow in Porous Media | 3 |
| ERPE 250 | Reservoir Engineering Fundamentals and Applications | 3 |
| ERPE 253 | Hydrocarbon Production System | 3 |
| ERPE 260 | Drilling Engineering | 3 |
| ERPE 270/ME 214 | Experimental Methods in Research | 3 |
| ERPE 310 | Sequence Stratigraphy | 3 |
| ERPE 311 | Carbonate Diagenesis | 3 |
| ERPE 315 | Energy Geoscience | 3 |
| ERPE 331 | Subsurface Geomechanics & Field Applications | 3 |
| ERPE 350 | Thermodynamics of Subsurface Reservoirs | 3 |
| ERPE 351 | Modeling Naturally Fractured Reservoirs | 3 |
| ERPE 360 | Field Development Planning | 3 |
| ERPE 361 | Advanced Well Testing | 3 |
| ERPE 362 | Enhanced Oil Recovery | 3 |
| ERPE 365 | Carbon Capture and Storage | 3 |
Elective Courses allow students to tailor their educational experience to meet individual research and educational objectives with the permission of the Academic Advisor. Students must select three Elective Courses from any 200/300 level courses at KAUST. ERPE core courses listed above can also be considered elective courses. The Courses listed below are most often selected by ERPE students as elective courses:
| AMCS 201 | Applied Mathematics I | 3 |
| AMCS 206 | Applied Numerical Methods | 3 |
| AMCS 231 | Applied Partial Differential Equations I | 3 |
| CS 201 | Introduction to Programming with Python | 3 |
| CS 229 | Machine Learning | 3 |
| ErSE 202 | Computational Groundwater Hydrology | 3 |
| ErSE 213 | Inverse Problems | 3 |
| ErSE 217 | Structural Geology | 3 |
| ErSE 222 | Machine Learning in Geoscience | 3 |
| ErSE 253 | Data Analysis in Geosciences | 3 |
| ErSE 260 | Seismic Imaging | 3 |
| ErSE 323 | Igneous Geochemistry | 3 |
| ErSE 327 | Multiscale Modeling of Geological Reservoirs | 3 |
| ErSE 330 | Pore-Scale Modeling of Subsurface Flow | 3 |
| ErSE 353 | Data Assimilation | 3 |
| STAT 210 | Applied Statistics and Data Analysis | 3 |
| STAT 220 | Probability and Statistics | 3 |
| STAT 230 | Linear Models | 3 |
| STAT 240 | Bayesian Statistics | 3 |
| STAT 250 | Stochastic Processes | 3 |
M.Sc. Degree Requirements:
The Master of Science (M.Sc.) degree is awarded upon successful completion of a minimum of 36 credit hours. A minimum GPA of 3.0 must be achieved to graduate.
The academic advisor must be a full-time program-affiliated assistant, associate, or full professor at KAUST. The academic advisor can only become project affiliated for the specific thesis project upon program level approval. Project affiliation approval must be completed prior to commencing research.
It is the sole responsibility of students to plan their graduate program in consultation with their advisor. Students are required to meet all deadlines and should be aware that most core courses are offered only once per year.
Individual courses require a minimum of a ‘B-’ for course credit. Students typically complete the M.Sc. degree within four semesters (18 months), however, they are strongly encouraged to complete the M.Sc. in three semesters (Fall, Spring, and Summer semesters, i.e., 12 months). Satisfactory participation in every KAUST's summer session is mandatory. Summer session courses are credit-bearing and apply towards the degree.
The non-thesis option is not supported by the ERPE Program. All M.Sc. students must conduct a capstone experience, including thesis preparation and oral defense.
- Core Courses (12 credits)
- Elective Courses (9 credits)
- M.Sc. Thesis Research or Research/Capstone Experience (15 credits) designed to provide students with the research experience
- Graduate Seminar (ERPE 398, non-credit) – a minimum of two ERPE 398 with Satisfactory grades must be completed within the duration of the MS degree. Students must attend a minimum of 8 Graduate Seminars to receive a Satisfactory (S) grade. The seminars can be chosen from any Graduate Seminar series offered by the PSE division. Students who fulfill the minimum requirement of two ERPE 398 do not need to register for additional Graduate Seminars. However, they are highly encouraged to attend the seminars.
- Successful completion of one Winter Enrichment Program (WEP)
Core and Elective Courses must be technical courses and cannot be substituted with Research, Internship, or Broadening Courses to fulfill degree requirements.
Students must have at least a 3.0 cumulative GPA. A minimum of 12 credits of thesis research (297) is required. Students are permitted to register for more than 12 credits of M.Sc. thesis research with the permission of the academic advisor. The selected academic advisor must be a full time program-affiliated assistant, associate, or full professor at KAUST. This advisor can only become project-affiliated for the specific thesis project upon program level approval. Project-affiliation approval must be completed prior to commencing research.
A written thesis and an oral defense of the M.Sc. thesis are required. It is advisable that students submit a final copy of the thesis to the thesis committee members at least two weeks prior to the defense date.
The thesis defense committee, which must be approved by the dean,
consists of three KAUST faculty. If additional expertise is needed, the
committee could be extended, subject to dean’s approval. At least two
committee members must be affiliated with the program. The chair may be
any KAUST faculty familiar with the program rules. This membership can
be summarized as:
| Member | Role | Program Status |
|---|---|---|
| 1 | Chair | Within or outside program |
| 2 | Faculty | Within program |
| 3 | Faculty | Within or outside program |
| 4 | Additional faculty or research scientist | Within or outside program |
Notes:
- Members 1, 2, and one of 3 or 4 are required
- Co-chairs may serve as member 2 or 3
- Adjunct professors and professors emeriti may retain their roles on current committees, but may not serve as chair on any new committees
- Professors of practice and research professors may serve as members 2 or 3 depending upon their affiliation with the student’s program, they may also serve as co-chairs
- Visiting professors may serve as member 3